Mathematical Modeling of diffusion:
Assuming that the diffusivities are independent of concentration, the relationship between the concentration of dopant (C) at any location (x) inside the wafer at any given time (t) is given by the following differential equation.

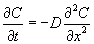
This is the simplified form of the equation called Fick’s second law, which describes the transient diffusion phenomenon.

In order to solve this equation, the appropriate boundary conditions must be given. There are two simplified cases that are applicable for diffusion in IC manufacturing. In one case, the concentration of the dopant is always maintained at the surface of the wafer. Inside the wafer, the concentration will change with time. This case is called “constant source” case. In the second case, the total quantity of doptant introduced is maintained constant, but the concentration of the dopant (at all locations, including the surface) will  change with time. This is called “limited source” case.

Constant source diffusion: Here, the concentration on the wafer surface is always equal to the solubility limit (Cs). The concentration at a location too far away from the surface (inside the wafer) is zero.  Before the beginning of diffusion process, the concentration of dopant in the wafer is zero. These are written as

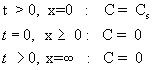
Sometimes this is also referred to as pre-deposition diffusion, because in those cases, diffusion will be done in two steps. The first step is called pre-deposition and the second step is called drive-in deposition. In the first step, a small quantity of impurity will be doped using the constant source mode and then the source will be removed. In the second step, the wafer will be maintained at high temperature for a certain time. The doped impurity will serve as the source and diffuse further in. Hence the first step is called the pre-deposition diffusion and the second step is called the drive-in diffusion.

For the constant source diffusion, the differential equation can be solved as follows.
Use the transformation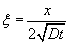
This leads to the following equation.

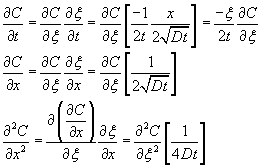
The original equation becomes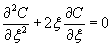  

The three boundary conditions reduce to two boundary conditions in the new variable

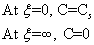
Let 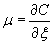. Then the above equation can be integrated as
This is integrated again to give

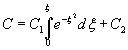
Here C1 and C2 are integration constants.

Using the boundary conditions, we get , C2=Cs and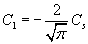

Complementary error function is defined as ,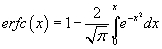

Thus,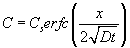