For many purposes, it is convenient to think of the symbols
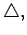
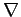
and

defined earlier, as operators,
which transform a given function
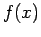
into related functions,
according to the laws:
In all these operations except D, the spacing h is implied.
Positive integral power of these operators are defined by
iteration. Also we define the zeroth power of any operator as the
identity operator I, which leaves any function
unchanged. For the operator
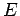
, the power
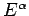
is defined
for any
real 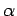
so that
while the
first form requires no explanation, the form
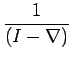
can be interpreted at this stage only as
representing the inverse of operator
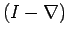
, that is, as an
alternative notation of the operator
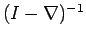
such that
![]()
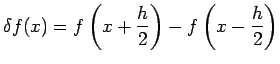
![$\displaystyle \mu
f(x)=\frac{1}{2}\left[f\left(x+\frac{h}{2}\right)+f\left(x-\frac{h}{2}\right)\right]$](img28.png)
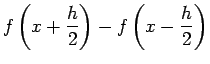
![$\displaystyle \frac{1}{2}\left[f\left(x+\frac{h}{2}\right)+f\left(x-\frac{h}{2}\right)\right]$](img53.png)
![$\displaystyle \frac{1}{2}\left[E^{\frac{1}{2}}f(x)+E^{\frac{-1}{2}}f(x)\right]$](img54.png)
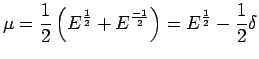
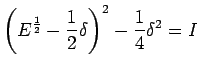
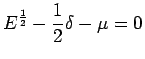
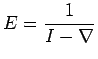
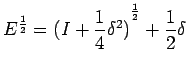
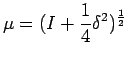
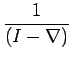 can be interpreted at this stage only as
representing the inverse of operator
can be interpreted at this stage only as
representing the inverse of operator
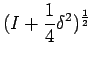 is to represent an
operator such that its iterate is the
operator
is to represent an
operator such that its iterate is the
operator
![$ \left[\left(I+\frac{1}{4}\delta^{2}\right)^{\frac{1}{2}}\right]^{2}=I+\frac{1}{4}\delta^{2}$](img72.png)