Next: Integrating Factors Up: Differential Equations Previous: Equations Reducible to Separable Contents
As remarked, there are no general methods to find a solution of (7.1.2). The EXACT EQUATIONS is yet another class of equations that can be easily solved. In this section, we introduce this concept.
Let ![]() be a region in
be a region in ![]() -plane and let
-plane and let ![]() and
and ![]() be real valued
functions defined on
be real valued
functions defined on
![]() Consider an equation
Consider an equation
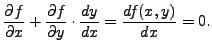
This implies that
The proof of the next theorem is given in Appendix 14.6.2.
Note: If (7.3.1) or
(7.3.2) is exact, then there is a function
![]() satisfying
satisfying
![]() for some constant
for some constant ![]() such
that
such
that
Let us consider some examples, where Theorem 7.3.4 can be used to easily find the general solution.
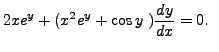
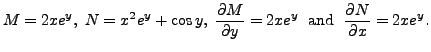
Therefore, the given equation is exact. Hence, there exists a function
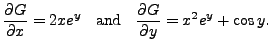
The first partial differentiation when integrated with respect to
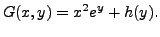
But then
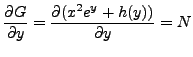
implies
The solution in this case is in implicit form.
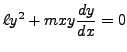
is exact. Also, find its general solution.
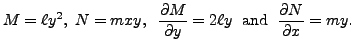
Hence for the given equation to be exact,
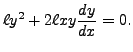
This equation is not meaningful if
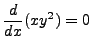
whose solution is
for some arbitrary constant
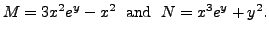
Hence,
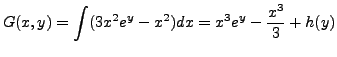
(keeping
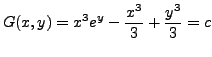
is the required implicit solution.