Next: Ordinary Differential Equation Up: Eigenvalues, Eigenvectors and Diagonalisation Previous: Diagonalisable matrices Contents
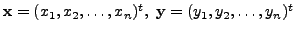 is an expression of the type
is an expression of the type
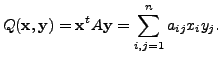
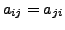 for all
for all
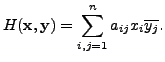
Note that if ![]() (the identity matrix) then the sesquilinear form reduces
to the standard complex inner product. Also, it can be easily seen that
this form is `linear' in the first component and `conjugate linear' in
the second component. Also, if we want
(the identity matrix) then the sesquilinear form reduces
to the standard complex inner product. Also, it can be easily seen that
this form is `linear' in the first component and `conjugate linear' in
the second component. Also, if we want
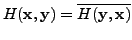 then the matrix
then the matrix ![]() need to be an Hermitian matrix. Note that
if
need to be an Hermitian matrix. Note that
if
![]() and
and
![]() , then the sesquilinear form reduces to a bilinear form.
, then the sesquilinear form reduces to a bilinear form.
The expression
![]() is called the quadratic form and
is called the quadratic form and
![]() the Hermitian form. We generally write
the Hermitian form. We generally write
![]() and
and
![]() in place of
in place of
![]() and
and
![]() , respectively. It can be easily shown that for any choice of
, respectively. It can be easily shown that for any choice of
![]() the Hermitian form
the Hermitian form
![]() is a real number.
is a real number.
Therefore, in matrix notation, for a Hermitian matrix ![]() , the
Hermitian form can be rewritten as
, the
Hermitian form can be rewritten as
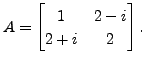 Then check that
Then check that 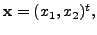 the Hermitian form
the Hermitian form
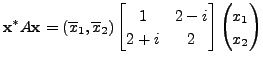 |
|||
![$\displaystyle \vert x_1\vert^2 + 2 \vert x_2\vert^2 + 2
{\mbox{Re}}[(2 - i) \overline{x}_1 x_2]$](img3118.png) |
The main idea is to express
![]() as sum of squares and hence determine
the possible values that it can take. Note that if we replace
as sum of squares and hence determine
the possible values that it can take. Note that if we replace
![]() by
by
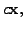 where
where ![]() is any complex number, then
is any complex number, then
![]() simply gets multiplied by
simply gets multiplied by ![]() and hence one needs to study only those
and hence one needs to study only those
![]() for which
for which
![]() i.e.,
i.e.,
![]() is a normalised vector.
is a normalised vector.
From Exercise 6.3.11.3 one knows that if ![]() (
(![]() is Hermitian) then there exists a unitary matrix
is Hermitian) then there exists a unitary matrix ![]() such that
such that
![]() (
(
![]() with
with ![]() 's the eigenvalues of the matrix
's the eigenvalues of the matrix ![]() which we know are real). So, taking
which we know are real). So, taking
![]() (i.e., choosing
(i.e., choosing ![]() 's as linear combination of
's as linear combination of ![]() 's with coefficients coming from
the entries of the matrix
's with coefficients coming from
the entries of the matrix ![]() ), one gets
), one gets
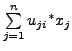 represents the principal
axes of the conic that they represent in the n-dimensional space.
represents the principal
axes of the conic that they represent in the n-dimensional space.
Equation (6.4.1) gives one method of writing
![]() as a sum of
as a sum of ![]() absolute squares of linearly independent
linear forms. One can easily show that there are more than one way of
writing
absolute squares of linearly independent
linear forms. One can easily show that there are more than one way of
writing
![]() as sum of squares. The question arises, ``what can
we say about the coefficients when
as sum of squares. The question arises, ``what can
we say about the coefficients when
![]() has been written as sum
of absolute squares".
has been written as sum
of absolute squares".
This question is answered by `Sylvester's law of inertia' which we state as the next lemma.
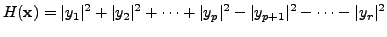
where
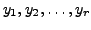 are linearly independent linear forms in
are linearly independent linear forms in
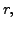
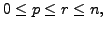 depend only on
depend only on
Hence, let us assume on the contrary that there exist positive integers
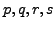 with
with 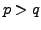 such that
/
such that
/
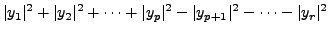 |
|||
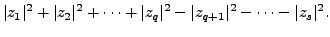 |
 and
and
 are linear combinations of
are linear combinations of
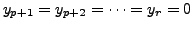 .
Since
.
Since 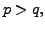 Theorem 2.5.1,
gives the existence of finding nonzero values of
Theorem 2.5.1,
gives the existence of finding nonzero values of
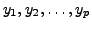 such that
such that
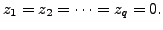 Hence, we get
Hence, we get
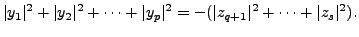
Now, this can hold only if
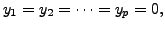 which gives a contradiction. Hence
which gives a contradiction. Hence 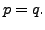
Similarly, the case 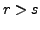 can be resolved.
height6pt width 6pt depth 0pt
can be resolved.
height6pt width 6pt depth 0pt
Note: The integer ![]() is the rank of the matrix
is the rank of the matrix ![]() and the number
and the number
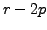 is sometimes called the inertial degree of
is sometimes called the inertial degree of ![]()
We complete this chapter by understanding the graph of
for
![$\displaystyle 3 x^2 + 4 x y + 3 y^2 = [x, \;\;
y] \begin{bmatrix}3 & 2 \\ 2 & 3 \end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}.$](img3156.png)
The eigenpairs for
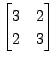 are
are
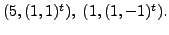 Thus,
Thus,
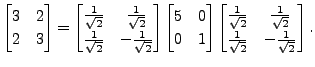
Let
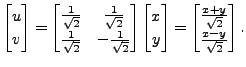
Then
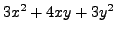 |
![$\displaystyle [x, \;\;
y] \begin{bmatrix}3 & 2 \\ 2 & 3 \end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}$](img3162.png) |
||
![$\displaystyle [x, \;\; y] \begin{bmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}...
...\sqrt{2}} &
-\frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix}x\\ y\end{bmatrix}$](img3163.png) |
|||
![$\displaystyle \bigl[ u, \;\; v \bigr] \begin{bmatrix}5
& 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix}u \\ v \end{bmatrix}$](img3164.png) |
|||
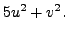 |
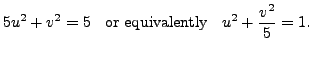
Therefore, the given graph represents an ellipse with the principal axes
The eccentricity of the ellipse is
![$\displaystyle a x^2 + 2h xy + b y^2 = \bigl[ x, \;\; y \bigr] \begin{bmatrix}a & h \\
h & b \end{bmatrix} \begin{bmatrix}x \\ y \end{bmatrix}$](img3176.png)
is called the quadratic form associated with the given conic.
We now consider the general conic. We obtain conditions
on the eigenvalues of the associated quadratic form to characterise
the different conic sections in
![]() (endowed with the standard inner
product).
(endowed with the standard inner
product).
Prove that this conic represents
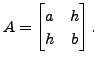 Then the associated quadratic form
Then the associated quadratic form
![$\displaystyle a x^2 + 2 h xy + b y^2 = \bigl[x \;\; y \bigr] A \begin{bmatrix}
x \\ y \end{bmatrix}.$](img3182.png)
As
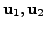 are orthonormal and
are orthonormal and
![$ \begin{bmatrix}u \\ v \end{bmatrix} = \bigl[ {\mathbf u}_1 \;\; {\mathbf u}_2 \bigr]
\begin{bmatrix}x \\ y \end{bmatrix}.$](img3185.png) Then
Then
and the equation of the conic section in the
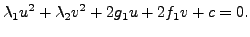
Now, depending on the eigenvalues
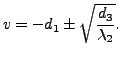
Also, observe that
![]() implies that the
implies that the
![]() That is,
That is,
![]()
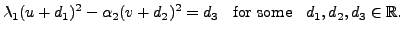
In this case, we have the following:
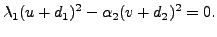
The terms on the left can be written as product of two factors as
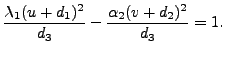
This equation represents a hyperbola in the
we now consider the following cases:
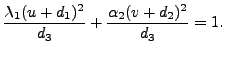
This equation represents an ellipse in the
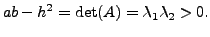
![$\displaystyle \begin{bmatrix}u \\ v \end{bmatrix} = \bigl[ {\mathbf u}_1 \;\; {\mathbf u}_2 \bigr]
\begin{bmatrix}x \\ y \end{bmatrix}$](img3230.png)
implies that the principal axes of the conic are functions of the eigenvectors
As a last application, we consider the following problem that helps us in understanding the quadrics. Let
where
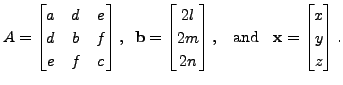
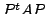 is a diagonal
matrix.
is a diagonal
matrix.
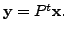 Then writing
Then writing
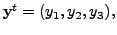 the equation (6.4.3) reduces to
the equation (6.4.3) reduces to
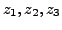 so that this equation is in the standard form.
so that this equation is in the standard form.
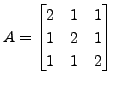 and
and
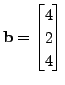 and
and 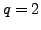 . Check that for the orthonormal
matrix
. Check that for the orthonormal
matrix
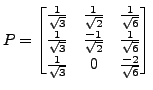 ,
,
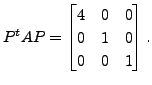 So, the equation of the quadric reduces to
So, the equation of the quadric reduces to
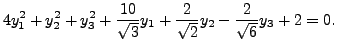
Or equivalently,
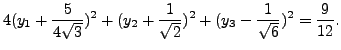
So, the equation of the quadric in standard form is
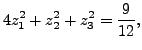
where the point
A K Lal 2007-09-12