Next: Diagonalisable matrices Up: Eigenvalues, Eigenvectors and Diagonalisation Previous: Introduction and Definitions Contents
Let ![]() be a square matrix of order
be a square matrix of order ![]() and let
and let
![]() be the corresponding linear transformation. In this section, we ask the
question ``does there exist a basis
be the corresponding linear transformation. In this section, we ask the
question ``does there exist a basis ![]() of
of
![]() such that
such that
![]() the matrix of the linear transformation
the matrix of the linear transformation ![]() is in the simplest possible
form."
is in the simplest possible
form."
We know that, the simplest form for a matrix is the identity matrix and the
diagonal matrix. In this section, we show that for a certain class of matrices
![]() we can find a basis
we can find a basis ![]() such that
such that
![]() is a diagonal matrix,
consisting of the eigenvalues of
is a diagonal matrix,
consisting of the eigenvalues of ![]() This is equivalent to saying that
This is equivalent to saying that
![]() is similar to a diagonal matrix. To show the above, we need the
following definition.
is similar to a diagonal matrix. To show the above, we need the
following definition.
![$ A= \left[\begin{array}{cc} 0 & 1 \\ -1 & 0
\end{array}\right].$](img2910.png) Then we have the following:
Then we have the following:
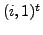 and
and
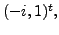 respectively. Also,
respectively. Also,
![$ U = \frac{1}{\sqrt{2}}\left[\begin{array}{cc}
i & -i \\ 1 & 1 \end{array}\right].$](img2917.png) Then
Then
![$\displaystyle U^* A U = \left[\begin{array}{cc} -i & 0 \\ 0 & i
\end{array}\right].$](img2918.png)
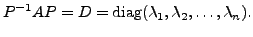
Or equivalently,
Since
Thus we have shown that if ![]() is diagonalisable then
is diagonalisable then ![]() has
has ![]() linearly
independent eigenvectors.
linearly
independent eigenvectors.
Conversely, suppose ![]() has
has ![]() linearly independent eigenvectors
linearly independent eigenvectors
![]() with eigenvalues
with eigenvalues
![]() Then
Then
![]() Let
Let
![]() Since
Since
![]() are linearly independent, by
Corollary 4.3.9,
are linearly independent, by
Corollary 4.3.9, ![]() is non-singular. Also,
is non-singular. Also,
![$\displaystyle [{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_n]
\begin{bmat...
...a}_2 & 0 \\ \vdots & \ddots & \vdots \\ 0 & 0 & {\lambda}_n \end{bmatrix}= P D.$](img2930.png) |
 . Then
. Then
Or equivalently
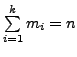 as
as
Now suppose that for each
![]() .
Then for each
.
Then for each
![]() , we can choose
, we can choose ![]() linearly independent eigenvectors.
Also by Corollary 6.1.17, the eigenvectors corresponding to distinct
eigenvalues are linearly independent. Hence
linearly independent eigenvectors.
Also by Corollary 6.1.17, the eigenvectors corresponding to distinct
eigenvalues are linearly independent. Hence ![]() has
has
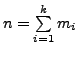 linearly
independent eigenvectors. Hence by Theorem 6.2.4,
linearly
independent eigenvectors. Hence by Theorem 6.2.4, ![]() is diagonalisable.
height6pt width 6pt depth 0pt
is diagonalisable.
height6pt width 6pt depth 0pt
![$ A=\left[\begin{array}{ccc}2 & 1 & 1\\ 1 & 2 & 1\\ 0 & -1
& 1 \end{array}\right].$](img2947.png) Then
Then
 It is easily seen that
It is easily seen that
![$ A=\left[\begin{array}{ccc}2 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1
& 2 \end{array}\right].$](img2953.png) Then
Then
 It can be easily
verified that
It can be easily
verified that
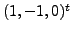 and
and
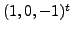 correspond to the eigenvalue
correspond to the eigenvalue
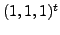 corresponds to the eigenvalue
corresponds to the eigenvalue 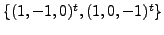 consisting of
eigenvectors corresponding to the eigenvalue
consisting of
eigenvectors corresponding to the eigenvalue 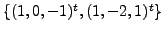 which still consists of eigenvectors corresponding to the eigenvalue
which still consists of eigenvectors corresponding to the eigenvalue ![$ U = \left[\begin{array}{ccc} \frac{1}{\sqrt{3}} &
\frac{1}{\sqrt{2}} & \frac{1...
...frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{2}}
& \frac{1}{\sqrt{6}} \end{array}\right]$](img2964.png) is the corresponding unitary
matrix then
is the corresponding unitary
matrix then
Observe that the matrix ![]() is a symmetric matrix. In this case, the
eigenvectors are mutually orthogonal. In general, for any
is a symmetric matrix. In this case, the
eigenvectors are mutually orthogonal. In general, for any
![]() real
symmetric matrix
real
symmetric matrix ![]() there always exist
there always exist ![]() eigenvectors and they are mutually
orthogonal. This result will be proved later.
eigenvectors and they are mutually
orthogonal. This result will be proved later.
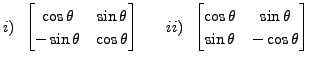 for any
for any 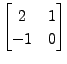 and
and
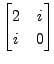 diagonalisable?
diagonalisable?
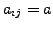 if
if 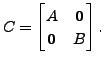 Then show that
Then show that
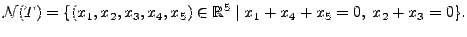
Then

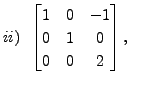
A K Lal 2007-09-12