Next: Matrix of a linear Up: Linear Transformations Previous: Linear Transformations Contents
Throughout this chapter, the scalar field
![]() is either always the
set
is either always the
set
![]() or always the set
or always the set
![]()
We now give a few examples of linear transformations.
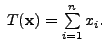
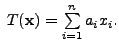 Note that examples
Note that examples
Then
for
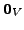 is the
zero vector in
is the
zero vector in 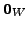 is the zero vector of
is the zero vector of
So,
From now on, we write
![]() for both the zero vector of the domain space
and the zero vector of the range space.
for both the zero vector of the domain space
and the zero vector of the range space.
Then
Then
We now prove a result that relates a linear transformation
![]() with its value on a basis of the domain space.
with its value on a basis of the domain space.
In other words, ![]() is determined by
is determined by
![]()
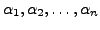 such that
such that
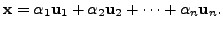 So,
by the definition of a linear transformation
So,
by the definition of a linear transformation
Observe that, given
That is, for every
![]()
![]() is
determined by the coordinates
is
determined by the coordinates
![]() of
of
![]() with respect to the ordered basis
with respect to the ordered basis ![]() and the vectors
and the vectors
![]() height6pt width 6pt depth 0pt
height6pt width 6pt depth 0pt
Then prove that
Show that for every
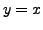 and
sends the point
and
sends the point
Is this function a linear transformation? Justify your answer.
Suppose that the map
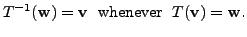
is a linear transformation.
Suppose there exist vectors
![]() such that
such that
![]() But by assumption,
But by assumption, ![]() is one-one and therefore
is one-one and therefore
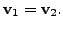 This completes the proof of Part
This completes the proof of Part ![]()
We now show that ![]() as defined above
is a linear transformation. Let
as defined above
is a linear transformation. Let
![]() Then by Part
Then by Part ![]() there exist unique vectors
there exist unique vectors
![]() such that
such that
![]() and
and
![]() Or equivalently,
Or equivalently,
![]() and
and
![]() So, for any
So, for any
![]() we have
we have
![]()
Thus for any
![]()
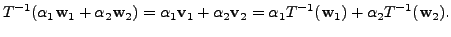
Hence
is called the inverse of the linear transformation
Note that
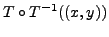 |
|||
for
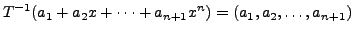
for
A K Lal 2007-09-12