3.10 Theory of Ionic Conduction
Now, having learnt the characteristics of ionic conduction and to know that ionic conductivity depends on the diffiusivity, we can now develop a theory for ionic conduction using Boltzmann statistics and see whether we arrive at the same formalism.
Here, we consider one dimensional movement of ions in a lattice as shown schematically in figure below. The distance between two ionic sites is d and in the absence of any field, the ions require to overcome an energy barrier of strength Ea or activation energy.
| Figure 3.6 Schematic diagram of the ionic movement in a lattice under application of a field |
In the absence of the any field, the probability of ion moving to its left or right, according to the Boltzmann statistics, is equal and is given as
Where α is the accommodation coefficient related to the irreversibility of the jump and ν is the vibrational frequency of the ions. Ea can be considered as activation energy or free energy change per atom.
Now when the field E is applied and if the ionic charge is z, then the force experience by the ion would be zeE. As a result for application of this force, the energy levels on the left and right of the ion would move up and down as show in the figure by a magnitude ½.F.d or ½ zedE, with total energy change being zeE.δ.
Now, the probability that the ion will move to its right is given as
Similarly, the probability of ion moving to its left would be
The above expressions shows that at any given temperature, the probability of the ion moving to right is higher than to the left i.e. 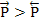 . This results in net motion of ions towards the right i.e. along the direction of the field and as a consequence, they acquire an average drift velocity, vav. This velocity is given as . This results in net motion of ions towards the right i.e. along the direction of the field and as a consequence, they acquire an average drift velocity, vav. This velocity is given as
Invoking a relation equivalent to 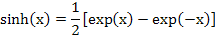 , we get , we get
Now, under normal circumstances and normal field for ceramic conduction, the field are quite small, a few V per cm and thus the field induced energy change is small as compared to the thermal energy i.e. 1/2 zeE.δ << kT. Using this we can modify above equation into
However, if 1/2 zeE.δ >> kT
Now, at low field strengths, assuming the validity of Ohm’s law, we write the current density as
where n is the ionic density per cc and total charge is ze.
Hence,
We know that P = α v exp [- Ea/kT].
Thus
Since, J = σ.E, we can write an expression for conductivity as
This expression has similar form that we worked out using diffusivity and mobility earlier and again show the similar dependence on temperature as well as activation energy for migration.
The following table shows activation energies for diffusion (kcal/mole) for a few oxides.4
| Table 3: Activation energy for diffusion for selected oxide ceramics |
Composition of Glass (mol%) |
Activation Energy (kCal/mol) |
Na2O |
CaO |
Al2O |
SiO2 |
|
|
33.3 |
- |
- |
66.7 |
13-14 |
14-16 |
15.7 |
- |
12.1 |
72.2 |
16.4 |
15.6 |
11.0 |
- |
16.1 |
72.9 |
15.6 |
15.1 |
15.9 |
11.9 |
- |
72.2 |
22.0 |
20.8 |
14.5 |
12.3 |
5.8 |
67.4 |
20.2 |
19.5 |
Good correspondence between activation energies for diffusion and dc conductivity shows that the model we just derived is also correct.
Conductivity of many β' and β''-alumina are very high and vary between 10 - 10-1 (Ω-cm)-1 over a temperature range of 300 K to 675 K. These also have typical activation energies between ~3.5-4.5 kCal/mole.
Spinel oxides such as Fe3O4 have conductivities of the order of 0.5 (Ω-cm)-1 and have very low activation energies, typically about 0.35 kCal/mole, representing almost temperature independent behaviour.
Compounds like Y2O3, HfO2, SiO2, Al2O3 are far more insulating and have conductivities in the range of 10-5 to 10-14 (Ω-cm)-1 in the temperature range of 400 K to 1000 K.
4Principles of Electronic Ceramics, L.L. Hench and J.K. West, Wiley, Table 4.2 |
|